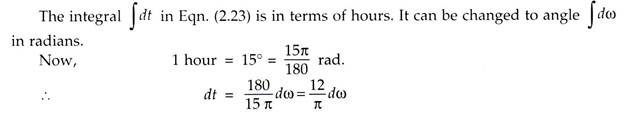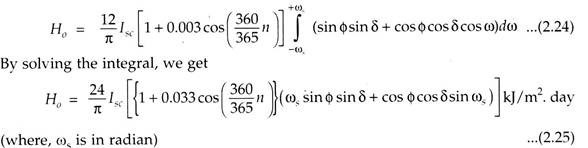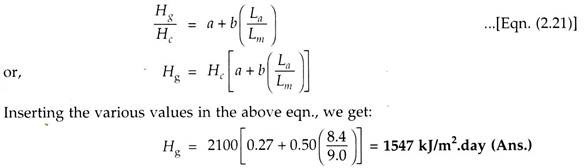Are you looking for an essay on ‘Solar Radiation’? Find paragraphs, long and short essays on ‘Solar Radiation’ especially written for school and college students.
Essay on Solar Radiation
Essay Contents:
- Essay on the Introduction to Solar Radiation
- Essay on the Types of Solar Radiation
- Essay on the Measurement of Solar Radiation
- Essay on Solar Radiation Data
- Essay on the Estimation of Average Solar Radiation
- Essay on Solar Radiation on an Inclined Surface
1. Essay on the Introduction to Solar Radiation:
The sun emits radiant energy as a spectrum corresponding to a ‘black body’ at a temperature of about 5500°C of which only a small amount is intercepted by the earth. Solar radiation is absorbed in the atmosphere and at the earth surface at a rate of 10.3 x 106 W.
The solar irradiance just outside the atmosphere is about 1353 W/m2. Because solar radiation is attenuated as it travels through the atmosphere, the total power falling on horizontal surface, known as the global irradiance, achieves a maximum of about 1000 W/m2 (i.e., IkW/m2) at sea level.
Global irradiance is actually made up of two components:
(i) “Direct beam radiation” from the sun and
(ii) “Diffuse radiation” from the sky (radiation that has been scattered by the atmosphere).
a. The amount of radiation received varies throughout the day as the path of solar radiation through the atmosphere lengthens and shortens. For the same reason, seasonal and lattitudal variations can cause the total solar energy received (known as insolation or solar irradiation) to range from an average of 2 MJ/m2/day (or 0.55 kWh/m2/day) in a northern winter to an average of 20 MJ/m2/day (or 5.55 kWh/m2/day) in the tropical regions of the world.
The diffuse energy may amount to only 15-20 percent of global irradiance on a clear day and 100 percent on a cloudy day.
b. The solar energy variability is important in system design and economics. Unlike conventional fossil fuel technologies, the performance of solar systems can vary markedly from one location to another. Consequently, to design a system to convert solar energy, one must have data on the solar radiation received at a particular site, preferably on a month-to-month basis.
If the system’s size is calculated from the yearly amount of solar energy, it may not provide energy output in months of low insolation, for convenience, the monthly solar radiation is usually expressed in terms of the daily average irradiation for the month; e.g., MJ/m2/day. Most available radiation data are for global irradiation; this is the starting point for assessing a site. If possible, data should be obtained from the nearest available meteorological station,and due allowance made for any localized micro-climate.
c. Solar radiation can be converted to other useful forms of energy, principally:
(i) Heat:
This can be used directly to heat or distil water or to dry crops. The relatively simple conversion can be carried out by means of a variety of solar thermal collectors,
(ii) Mechanical or Electrical Power:
These two forms, which are easily and efficiently interconvertible, can serve a variety of end-uses, including water pumping, lighting and refrigeration.
However, the energy conversion technology is much more complex than that of heat production.
Conversion can be achieved by two completely different routes:
(i) Solar thermodynamics.
(ii) Solar photovoltaic.
Conditions for utilization of solar energy, in India, are favourable since for nearly six months of the year sunshine is uninterrupted during the day, while in the other six months cloudy weather and rain provide conditions suitable for water power. Thus, a coordination of solar energy with water power can provide a workable plan for most places in India.
Following renewable energy sources find their origin in ‘Sun’:
(i) Wind
(ii) Ocean thermal
(iii) Ocean wave
(iv) Ocean tide
(v) Geothermal
(vi) Biomass
(vii) Organic chemicals
(viii) Fossil fuels.
2. Essay on the Types of
Solar Radiation:
Solar radiation is the energy radiated by the sun.
i. The radiated energy received on earth surface is called Solar irradiation.
ii. Solar radiation received on a flat horizontal surface on earth is called Solar insolation.
The solar radiation is of the following two types:
1. Extra-Terrestrial Solar Radiation:
The intensity of sun’s radiation outside the earth’s atmosphere is called “extra-terrestrial” and has no diffuse components.
Extra-terrestrial radiation is the measure of solar radiation that would be received in the absence of atmosphere.
2. Terrestrial Solar Radiation:
The radiation received on the earth surface is called “terrestrial radiation” and is nearly 70 percent of extra-terrestrial radiation.
Spectral Distribution of Solar Radiation:
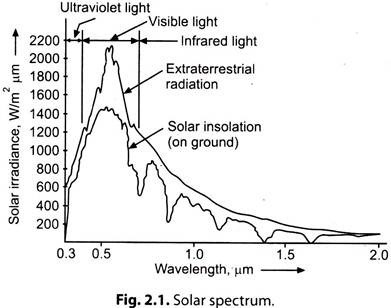
Light rays radiated from the sun are in the form of electromagnetic waves in infrared, visible and ultraviolet frequence bands. The frequency spectrum of solar light is a graph of wavelength against power density, shown in Fig. 2.1.
The solar spectrum has the following three basic levels:
(i) “Infrared band” with wavelengths too long for response by human eye (frequency range: 4 x 1014 to 7.5 x 1010 Hz) wavelengths: between 0.75 micron and 1.95 microns (1 micro, µm = 10-6 m).
(ii) Visible band: Frequency range: 6 x 1016 to 7.69 x 1014 Hz; Wave lengths: Between 0.39 micron and 0.75 micron.
(iii) Ultraviolet band: Frequency range: 6 x 1016 to 7.5 x 1014 Hz.
Wavelengths: Between 0.005 micron to 0.39 micron.
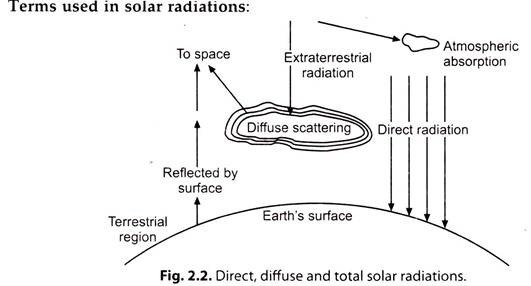
Refer to Fig. 2.2.
Beam (or Direct) Radiation (Ib):
Solar radiation received on the surface of earth without change in directions is known as “beam or direct radiation”.
Diffuse Radiation (Id):
The solar radiation received from the sun after its direction has been changed by reflection and scattering by atmosphere is known as “diffuse radiation”.
Total Radiation (IT):
The sum of beam and diffuse radiations intercepted at the surface of earth per unit area of location is known as “total radiation”. It is also known as “Insolation”.
Mathematically: IT = Ib + Id …(2.1)
Airmass (ma):
It is the path length of radiation through the atmosphere, considering the vertical path at level as unity.
ma = 1, when sun is at zenith (i.e., directly above head).
ma = 2, when zenith angle (θZ) is 60°.
ma = sec θz, when ma > 3
ma = 0 just above the earth’s atmosphere
“Reasons for variation in solar radiations reaching the earth than received on the outside of the atmosphere”:
As solar radiations pass through the earth’s atmosphere the shortwave ‘intraviolet rays’ are ‘absorbed’ by ozone in atmosphere and the long wave infrared waves’ are ‘absorbed’ by carbon dioxide and moisture in the atmosphere. A portion of radiations is ‘scattered’ by the components of atmosphere such as water vapour and dust. A portion of this scattered radiation always reaches the earth’s surface as ‘diffuse radiation’. Thus radiations finally received at the earth’s surface consists partly of beam radiation and partly of diffuse radiation.
3. Essay on the Measurement of Solar Radiation:
It is important to measure solar radiation, owing to the increasing number of solar heating and cooling applications, and the necessity for accurate solar radiation data to predict performance.
The following three devices are used for measuring the solar radiations:
1. Pyranometer;
2. Pyrheliometers;
3. Sunshine recorders.
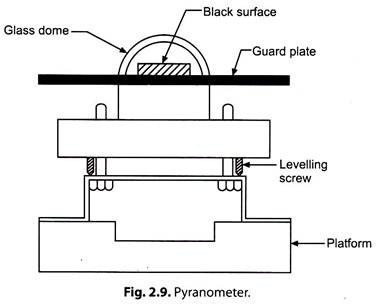
1. Pyranometer:
A pyranometer is a device used to measure the “total hemispherical solar radiation”. The total solar radiation arriving at the outer edge of the atmosphere is called the ‘solar constant’.
The ivorking principle of this instrument is that sensitive surface is exposed to total (beam, diffuse and reflected from the earth and surrounding) radiations.
The description of a pyranometer is given below:
Refer to Fig. 2.9.
Construction of Pyranometer:
It consists of a “black surface” which receives the beam as well diffuse radiations which rises heat. A “glass dome” prevents the loss of radiation received by the black surface. A “thermopile” is a temperature sensor, and consists of a number of thermocouples connected in series to increase the sensitivity. The “supporting stand” keeps the black surface in a proper position.
Working of Pyranometer:
When the pyranometer is exposed to sun, it starts receiving the radiations. As a result, the surface temperature starts rising due to absorption of the radiation. The increase in the temperature of the absorbing surface is detected by the thermopile. The thermopile generates a thermo emf which is proportional to the radiations absorbed; this thermo emf is calibrated in terms of the received radiations. This will measure the global solar radiations.
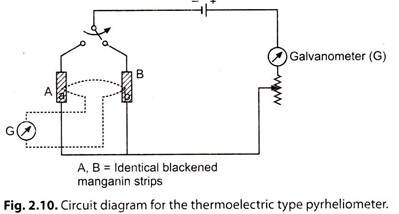
2. Pyrheliometer:
A pyrheliometer is a device used to measure “beam or direct radiations”. It collimates the radiation to determine the beam intensity as a function of incident angle.
This instrument uses a collimated detector for measuring solar radiation from the sun and from a small portion of the sky around the sun at normal incidence.
The description of a thermoelectric type pyrheliometer is given below:
Refer to Fig. 2.10.
Construction of Pyrheliometer:
In this instrument, two identical blackened manganin strips A and B are arranged in such a way that either can be exposed to radiation at the base of collimating tubes by moving a reversible shutter.
Working of Pyrheliometer:
One strip is placed in radiation and a current is passed through the shaded strip to heat it to the same temperature as the exposed strip. When there is no difference in temperature the electrical energy supplied to shaded strip must equal the solar radiation absorbed by the exposed strip. Solar radiation is then determined by equating the electrical energy to the product of incident solar radiation, strip area and absorptance.
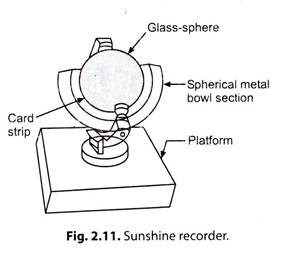
3. Sunshine Recorder:
A sunshine recorder is a device used to measure the “hours of bright sunshine in a day”.
The description of a sunshine recorder is given below:
Refer to Fig. 2.11.
Construction of Sunshine Recorder:
It consist of a “glass-sphere” installed in a section of “spherical metal bowl” having grooves for holding a recorder card strip and the glass sphere.
Working of Sunshine Recorder:
The glass-sphere, which acts as a convex lens, focuses the sun’s rays/beams to a point on the card strip held in a groove in the spherical bowl mounted concentrically with the sphere.
Whenever there is a bright sunshine, the image formed is intense enough to burn a spot on the card strip. Through the day, the sun moves across the sky, the image moves along the strip. Thus a burnt space whose length is proportional to the duration of sunshine is obtained on the strip.
4. Essay on Solar Radiation Data:
General Aspects of Solar Radiation Data:
Solar radiation data should include the following information:
(i) Whether they are instantaneous measurements or values integrated over some period of time (usually hour or days,)
(ii) The time or time period of the measurements;
(iii) Whether the measurements are of beam, diffuse or total radiation and the instrument used;
(iv) The receiving surface orientation (usually horizontal, it may be inclined at a fixed slope or normal);
(v) If averaged, the period over which they are averaged.
An instrument called Solarimeter is used to measure most of the data on solar radiation received on the surface of the earth. It gives readings for instantaneous measurements at rate throughout the day for total radiation on a horizontal surface. Integrating the plot of rate of energy received per unit area per unit time over a whole day gives the “langleys” of radiation received on a horizontal surface (the unit ‘langley’ has been adopted in honour of Samuel Langley who made the first measurement of the spectral distribution of the sun; 1 langley = 1 cal/cm2).
i. When data are not available, ‘Maps’ can be used as a source of average radiation. Charts are also available for clear day horizontal radiation for any period for any latitude. Tables are also available for hours of sunshine for various locations.
ii. The solar radiation data is collected for various locations in the world on the basis of:
1. Solar power calculations with reference to the movement of the sun, latitude of the location etc.
2. Hourly measurements of solar radiation at the location and calculation of:
a. “Daily average” global radiation (Hdg) at the location for the month (kJ/m2Jay);
b. “Monthly average” global radiation (Hmg) at the location for various months (kj/ m2. month); (iii) “Yearly average” global radiation (Hyg) at the location for a few years (kJ/m2. year).
The data in terms of kj/m2. day or kWh/m2. day for various days/months/an year can be readily used for calculating:
(i) Available solar energy at the location;
(ii) Determining the surface area of the solar collectors;
(iii) Determining rating of solar plant.
Solar Radiation Data for India:
(i) India is in the “northern hemisphere” within latitudes of 7° and 37.5° N.
(ii) The average solar radiation values for India are between 12.5 and 22.7 MJ/m.” day.
(iii) The peak solar radiation in India occurs in some parts of Rajasthan and Gujrat and is equal to 25 MJ/m2.
(iv) The solar radiation reduces to about 60 percent during monsoon months.
Solar Insolation:
The solar insolation is the solar radiation received on a flat horizontal surface at a particular location on earth at a particular instant of time. The unit of solar radiation is W/m2.
The parameters of the solar insolation for a given flat horizontal surface are:
(i) Daily variation (hour angle);
(ii) Seasonal variation and geographical location of the particular surface;
(iii) Atmospheric clarity;
(iv) Shadows of trees, tall structures, adjacent solar panels etc.;
(v) Degree of latitude for location;
(vi) Surface area m2;
(vii) Tilt angle.
5. Essay on the Estimation of Average Solar Radiation:
“Angstrom’s Equation” for Average Daily Global Radiation:
The expression for the average radiation on a horizontal surface in terms of constants a and b and observed values of average length of solar days, as suggested by Angstrom (1924) is given by:
where, Hg = Monthly average of the daily global radiation on a horizontal surface at the location (kJ/m2 day),
Hc = Monthly average of the daily global radiation on the same horizontal
surface at the same location but on clear sky day (kJ/m2. day),
a, b = Constants determined from various cities in the world by measurements,
La = Average length of solar day for a particular month calculated/observed (hours), and
Lm = Length of the longest solar day in the month (hours).
Modified Angstrom’s Equation:
The modified Angstrom’s equation is written by replacing Hc by H0 in Eqn. (2.21) as:
where, H0 = Monthly average of the daily extra-terrestrial radiation, which would fall on a horizontal surface at the location under consideration (kj/m2. day).
The expression for H0 is given by:
where, n = Number of days in the year,
Isc = Solar constant = 4870.8 kJ/m2 hour,
ɸ = Angle of latitude for the location,
δ = Angle of declination of equatorial plane, and
ω = Hour angle for local apparent time.
Inserting the value of dt in Eqn. (2.23), and integrating between sunrise (- ωs) to sunset (+ ωs) for total day light period, we get:
From Eqn. (2.25), the value of H0 is calculated in terms of kJ/m2. day for a clear sky day, for a flat surface location.
Hence, the value of Hg (Daily global radiation-monthly average) for a horizontal surface at the location is then calculated by using the values of H0, a, b in Eqn. 2.22.
H0 can be obtained from charts or can be calculated by the following Empirical relation:
where, Isc = Solar constant per hour,
n = Day of the year, and
ωs = Sunrise hour angle (degrees).
The ‘declination 5’ can be obtained from ‘Cooper equation’ and the sunrise hour angle (i.e., ωs) from the following equation:
ωs = — tan ɸ tan δ
Example 1:
The following observations were made in Bhopal during the mouth of March- Average length of the day = 8.4 hours; Longest day during the month = 9 hours; Angstrom’s constants for Bhopal: a = 0.27, b = 0.50; Solar radiation per day for a clear day = 2100 J/m2 day. Calculate the average daily global radiation.
Solution:
Given- La = 8.4 hours, Lm = 9 hours; a = 0.27; b = 0.50;
Hc = 2100 J/m2. day.
Average Daily Global Radiation, Hg:
Angstrom’s equation is written as:
Example 2:
Calculate the average value of solar radiation on a horizontal surface located in Ahmedabad (22°00’N, 73° 10’E), for May 28. Average solar day hours are 10.5 hours. Angstrom’s constants are: a = 0.28, b = 0.48.
Solution:
Given: ɸ = 22°, Average solar day hours La = 10.5 hours; Angstrom’s constants: a = 0.28, b = 0.48.
Monthly average of daily global radiation, Hg:
6. Essay on Solar Radiation on an Inclined Surface:
The following three types of solar radiation constitute the total solar radiation on a surface:
(i) Beams solar radiation (Ib);
(ii) Diffuse solar radiation (Id);
(iii) Solar radiation reflected from the ground and the surroundings.
Usually, 4 and ld on a horizontal surface are recorded.
In case of non-availability of data for beam and diffuse radiation, the following expression for beam and diffuse radiation on the horizontal surface may be used:
4 = IN cos θZ …(2.27)
and, Id = 1/3(Iext,-IN)cosθ2 …(2.28)
Li and Jordon (1962) suggested the following formula to evaluate total radiation on a surface of “arbitrary orientation”-
IT = IbRb + IdRd +p Rr (Ib + Id) ….(2.29)
where, Rb, Rd and Rr = “Conversion factors” for beam, diffuse and reflected components respectively; p = The reflection coefficient of the ground = 0.2 and 0.7 for ordinary and snow covered ground respectively.
Expressions for Conversion Factors:
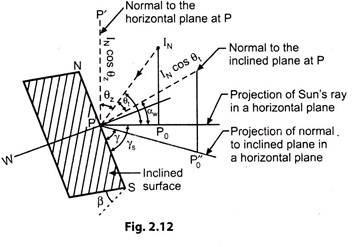
Refer to Fig. 2.12.
(i) Rb:
It is defined as the ratio of flux of beam radiation (Ib) incident on an inclined surface (Ibt)to that on a horizontal surface. It is called tilt factor for beam radiation.
(ii) Rd:
It is the ratio of the flux of diffuse radiation falling on the tilted surface to that on the horizontal surface.
If one “radiation shape factor” for the tilted surface with respect to sky, is
(iii) Rr:
The reflected component comes mainly from the ground and other surrounding objects. If the considered reflected radiation is diffuse and isotropic, then the situation is opposite to that in the above case, and
where p = Reflection coefficient of the ground (0.2 for ordinary and 0.7 for snow covered ground).
Hence combining all the three terms, we get: