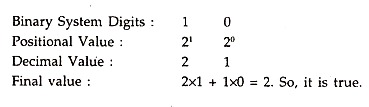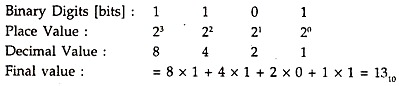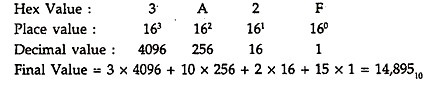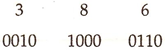Are you looking for an essay on the ‘Number System’? Find paragraphs, long and short essays on the ‘Number System’ especially written for school and college students.
Essay on the Number System
Essay Contents:
- Essay on the Binary Number System
- Essay on the Hexadecimal Number System
- Essay on the Octal Number System
- Essay on the Binary Coded Decimal
Essay # 1. The Binary Number System:
In mid-1940s John von Neumann along with H.H. Goldstein and A.W. Buifks proposed a new number system using two digits called Binary Number System and it readily became the basic number system for computer operations.
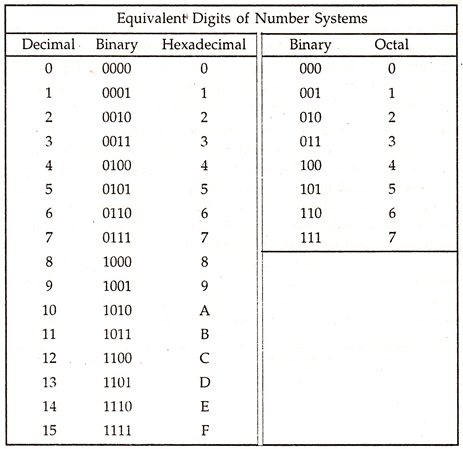
A number system using two digits, under the basic concept, will have a base (radix) of two and its highest digit will be [Number of Digits in the System minus 1] or [2-1] = 1; the other digit being 0. Thus, the Binary Number System has two digits, 0 and 1, 0 representing the off-position and 1 representing the on-position of a two state device—the 0 and 1 are called Binary digits or Bits in short.
But since, a single bit can represent only two different positions, so the switches are always used in combinations to give larger number of options. When 4 bits, called nibble, are used together we can get 24 = 16 different combinations; with 8 bits, called a byte, we get 28 = 256 combinations; and with 16 bits, called a word, we get 216 = 65,536 positions. Incidentally, a kilo in binary system is 210 = 1024, and not 1000.
Since writing 16 or 32 bits of 0s and Is is a bit cumbersome, difficult to remember, with chances of mistakes being high, a short-hand version called Hexadecimal Number System has been developed, where 4 binary digits are represented by one digit of the hexadecimal system—which uses 16 digits : 0 to 9, and A to F, with A being 10 and F being 15, the others coming in between.
As far as the binary and the decimal systems are concerned, the digits 0 and 1 are common in both the systems, but there after they differ, as in the binary system the highest digit is 1 and in the decimal system it is 9. To get the value of two in the decimal system, we add 1 with 1 to get 2.
Similarly, in binary system we will have to add 1 with 1—but we cannot write 2, as we do in the decimal system. What is the way out? In the decimal system, when we add 1 to the highest digit of 9, we write 0 in unit’s place and carry over 1 to the ten’s place, the value of the digit changing to 10.
Thus we have:
But is it really true?
Let’s check by computing the place values under the binary system. The base value of the binary system being 2, the positional value will be 20 for LSD [Least Significant Digit] and there after 21 = 2, 22 = 4, 23 = 8, 24 = 16, and so on, as we move from right to left in a group of digits; corresponding to 100, 101, 102, 103 etc. of the decimal system.
Then:
We know that 1101 in decimal system represents one-thousand-one-hundred-one.
In Binary Number System, the same group of digits will be evaluated as:
The subscript 10 indicates that the digit 13 is in decimal system. Thus we can convert any binary number, which the computer understands, to get the equivalent decimal number which we easily understand. How about binary fractions, which are less than 1 in value? The same logic as was used in the decimal system is followed, but now, obviously, with a base of 2.
In decimal system we use position numbers as negative power of base 10 to get 10―1, 10―2, 10―3 and so on. In binary system, correspondingly we have 2―1, 2―2, 2―3 etc. as we move further to the right from the binary-point, which we called decimal-point earlier. Thus for 1101—
Decimal to Binary Conversion:
As you saw, converting binary digits, or bits, to decimal numbers was a fairly straight forward process—we just added the place values, ignoring it when the bit was 0. To convert decimal numbers to equivalent binary numbers, we follow a popular process called double- dabble method.
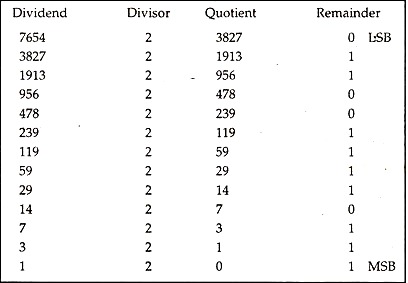
Under this procedure, we successively divide the decimal number by 2, noting down the remainder in each case serially, starting with the first remainder which is called LSD or more appropriately LSB—Least Significant Bit. The division stops when the quotient becomes 0. Let us find out the bits to represent 765410.
Therefore, the equivalent binary number is 11101111001102,
Let us check it by reconverting to decimal number.
The above method is also called Remainder Method by some.
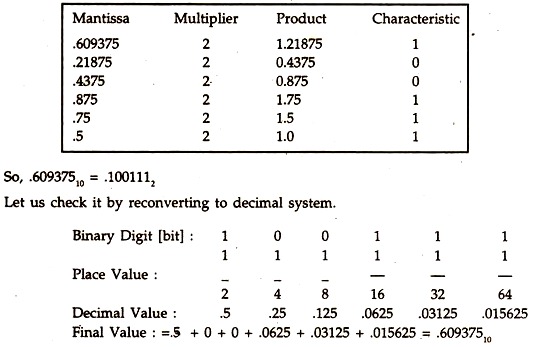
To convert the fractional part of the decimal system to its equivalent bits, which are written after the binary point, instead of resorting to repeated division by 2 as we did in the double-dabble method, we reverse the process by repeatedly multiplying the fractional part by 2.
The product so obtained consists of two parts—an integer before the decimal point called characteristic, which would be either 0 or 1 [here] and another fractional part called mantissa. The characteristic of each product gives the binary digit required, the remaining mantissa is again multiplied likewise; the first characteristic so obtained is placed after the binary point. Let us convert 0.60937510 to equivalent binary digits.
Binary Addition:
Binary addition is extremely simple being identical to the decimal system, except, the carry-over of 1 takes place whenever the result of summation is greater than 1— in decimal system, the carry-over of 1 is done whenever the sum is greater than 9 (the highest digit in the system). Let us take a few examples. In each case the decimal equivalent is also given.
The basis principle in binary system is: 0+0 = 0; 0+1 = 1; 1+1 = 10
Essay # 2. Hexadecimal Number System:
Although the computers operate on binary system of Is and 0s used in combinations, it was found that with increase in processing ability and storage capability, using so many 0s and Is for each data/instruction was a tedious process, difficult to remember, and the possibility of mistake was very high, resulting in disastrous results.
In a PC, 16 bits are used for normal working with PC AT operating at 32 bits level. So any data or instruction would normally require to be represented by a combination of 16 or 32 bits of 0s and 1s. To find an easy way out as far as programmers are concerned, a short-hand substitute, another number system has been developed, called Hexadecimal System or Hex in short, which uses 16 digits.
Now, where do we get 16 numbers of single digits? 0 to 9 provides only ten digits. We cannot use 10, 11, etc. as these are combinations of basic digits of 0 and 1 and they occupy two places. The solution was found, selecting the first five alphabets, A to F—A being 10, B being 11, C being 12,’D being 13, E being 14, and F being 15, the largest digit— the base of the system being 16.
The system has a unique advantage that exactly 4 binary digits (a nibble) is represented by a single hex digit, the F being represented by 11112—a byte consisting of 8 bits is fully represented by 2 hex digits. If you peep into a computer’s primary memory using any software like Debug, PCTools, or Norton Utility, you will find everything being represented in hexadecimal numbers.
Note that two hex digits are required to represent a byte and very large decimal numbers can be represented by only a few hex digits. You should be proficient in interpreting hex digits, if you are serious about being a computer expert. It is a must.
Hexadecimal to Decimal Conversion:
Our basic number system being the decimal system, we have to know how to convert the hexadecimal numbers to decimal [and also binary system] and vice versa.
The process of conversion to decimal system is similar to that for the decimal to binary system, with the following exceptions:
1. The base here is obviously 16, instead of 2.
2. In binary system, the digits were either 0 or 1, so we either added or rejected the place values, depending on whether it was 1 or 0. But in hexadecimal system, each position may have any digit between 0 and F [15], so the respective digits have to be multiplied with corresponding place values to get the final values; as we did in the decimal system for expanded notation.
For example, to convert 3A2F to decimal system, we write:
In case of conversion of hexadecimal number to binary number, we simply write down the corresponding bits, as shown below:
It should be noted that since 4 bits make a hex digit, all the 4 bits need to be written, like 0001 for 1.
Decimal to Hexadecimal Conversion:
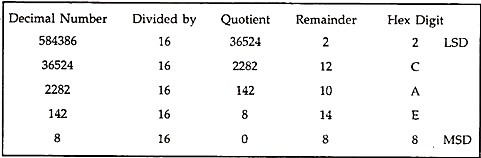
This process is also identical with that for binary system, except instead of 2, we divide by 16 to get the remainders, which represent hex digits.
To convert 584386 to hexadecimal:
Therefore, 58438610 = 8EAC216
Essay # 3. Octal Number System:
Some of the earlier computer systems had adopted a configuration under which six binary digits were taken to form a byte (now it is 8 bits to a byte). Hence, they developed the octal number system, whereby two octal digits fully represented their bytes; as two hex digits now represent a byte.
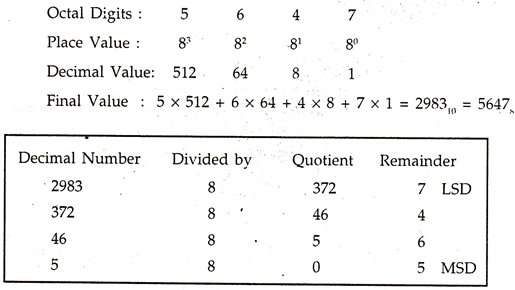
Under the system, as the name suggests, there are eight digits, with the highest one being [8 – 1] = 7 and, naturally, the base is 8. Since three binary digits can fully represent 0 to 7, an octal digit can be represented by three bits—111, = 7S.
Octal to Decimal and Back:
By now all of you should be fully proficient to tackle any number system, so two representative examples are given for symbolic reference.
The octal equivalent is 56478.
Essay # 4. Binary Coded Decimal:
No matter how scientific and useful a number system is, we always feel a bit comfortable working with the decimal number system. Hence, a number of code systems have been developed to integrate the two number systems of decimal and binary—so that we operate in decimal system and the computer continues with the binary system, the codes facilitating conversion from one form to the other.
These codes are called Binary Coded Decimals [BCD], A large number of such codes exist. Under these systems, individual decimal digits are converted to equivalent binary form, instead of the total decimal value being converted to its binary equivalent. The most popular one is called the 8-4-2-1 code.
In this system, each decimal number is expressed in binary form using its equivalent binary digit using 4 bits, like 0001 for 1, 0100 for 4, 1001 for 9. The weights given to the bit positions are 8, 4, 2, and 1, respectively and so it is called 8-4-2-1 code.
The decimal 386 in binary form using 8-4-2-1 code would be as:
By using this code the numbers of one system can be easily converted to the other system conveniently, but rules of binary arithmetic becomes invalid with such numbers. [Under proper binary conversion 386 would become 1 1000 0010].