Are you looking for an essay on ‘Computer Programming’? Find paragraphs, long and short essays on ‘Computer Programming’ especially written for college and IT students.
Essay on Computer Programming
Essay Contents:
- Essay on the Definition of Computer Programming
- Essay on the Steps Involved in Computer Programming
- Essay on Modular Programming
- Essay on Preparing a Program Flow-Chart
- Essay on Decision Table for Pre-Programming Sequencing
- Essay on Logical Instruction Used in Computer Programming
Essay # 1. Definition of Computer Programming:
A program may be defined as a sequence of instructions given to the computer. The instructions are recorded in the language of the computer on a proper medium such as card, disk or tape which the computer may read. It is the program by which the whole operations of the computer are directed and controlled.
The work of programming begins with considering the nature of the solution or end results desired, then tracing in specific detail (each small step) the processing steps needed to produce the desired results, and finally expressing the program in a language that can be understood and followed by the particular computer.
The principal steps in programming are given below:
1. Developing a general flow chart. It indicates the input-output expected from the programme.
2. Developing a detailed flow chart of the functions. The components must perform to obtain the desired results. A block diagram may be prepared to graphically represent the procedures by which data are processed within a system.
3. Preparing the programme of instructions in a form and sequence usable by the computer.
The computer language may be either machine-oriented, or problem-oriented.
A machine-oriented language can be used only on the computer for which it has been designed. This language contains alphabetic codes which are known as un-numeric codes. It is easier to remember un-numeric codes than numeric codes. So it is easier to write a program in this language.
These days problem-oriented languages have also been developed which can be used in programming for a variety of computers.
Some of the commonly used computer languages are briefly described below:
(a) Fortran (Formula Translator):
It is an automatic coding system that resembles the ordinary language of mathematics. It is capable of expressing any numerical problem in computer language and is mainly used for solution of mathematical problems.
(b) Cobol (Common Business Oriented Language):
It is the simplest of all the computer languages. It closely resembles a common English statement. It is most commonly used in solution of business data processing problems.
(c) Basic (Beginners All-Purpose Symbolic Instruction Code):
It is an easy- to-use language whose instructions resemble elementary algebraic formulas, augmented by certain English keywords such as read, print, go to, if, then, etc. It is well suited for persons learning to programme for the first time. It is widely used in areas of business, economics, medicine, science and technology, etc.
(d) Other Languages:
There are many other programming languages such as ALC (Assembler Language Coding), ALGO (Universal Algebraic Language Compiler), ALGOL (International Algebraic Compiler), PL/I, Pascal etc.
Essay # 2. Steps Involved in Computer Programming:
Below mentioned are the steps involved in programme development:
i. Problem Identification:
Identifying or defining the problem in correct perspective—the output to be provided by the program to the user. In fact, the solution of many problems becomes crystal clear if the problem is correctly defined. The job of problem identification comes under the broad category of System Analysis.
ii. Task Analysis:
Once the problem has been identified in terms of output, without going into the details of how the output will be actually produced from the input, the next step is identifying the tasks which would process or manipulate the data to produce the output desired. Any large job can be broken down to easily process-able smaller tasks, the cumulative effect of which is to provide the final outcome.
Even the three basic operations of input, processing, and output usually have smaller components which can be treated as small programming modules.
For example, in the input operation, there could be one module for adding new data to the file, another module to modify the existing data, and so on. The objective of task analysis is to break down the main job to a number of smaller tasks to make the programming simpler.
iii. Pre-Program Sequencing:
So far the steps involved have been restricted to problem-identification and task-analysis, detailing the steps required to generate the output from the planned input, but in a manner as any human beings would do with pen, paper, ruler, and calculator.
Since our objective is to get the job done by a computer, whose processing abilities are somewhat restricted compared to us, we now have to detail the steps in a manner as the computer will actually do it, but still expressing the instructions in our own natural language.
When this part will be completed, all that would remain to be done to bring the program into existence, would be to use the codes of any high level language to translate the instructions into computer process-able codes—which the compiler or interpreter will translate into machine readable codes.
Such type of codes, which represents the actual processing codes of a computer in a natural language is called pseudo-code; giving the outline of the program. Let us say that we want a program to compute the area of a circle. After the first two steps of program development, under pre-program sequencing we may write—
For a radius R, the area of a circle is nR2 and by using different values of R, we will get different areas and we also know n = 3.14 [approximately].
In terms of pseudo-code, we would write:
a. Get the value of the radius R from the user
b. Define a constant PAI = 3.14
c. Compute the Area, A = PAI x R x R
d. Display the value of A.
These four steps provide the detail of different instructions to be given to a computer, which will ultimately be converted into machine understandable form, after being coded using the syntax of a high level language.
A number of aids are available, which are frequently used to prepare the foundation or outline of a program, which then is coded. One such aid is called Flow Chart, which is a graphical representation of the steps of the instructions leading to the solution, using standard symbols.
Another aid in understanding the correctness of logical operations by a computer for solving problems is called Decision Table—it helps to clearly express the situations where the processing is dependent on fulfilment of certain conditions, like say, display the name of the employee whose salary is below Rs. 2,000/- at an age of above 55 years.
iv. Program Coding:
The next step in program development is to convert the pseudo-codes to the specific programming language codes based on the syntax and semantics of the commands of the language. The word syntax refers to the way the commands are to be used correctly, as provided in the language being used— which are called formal or artificial language, as the words used by them have clear predefined rules.
Semantics refers to the meaning of a command, or in other words, what will be the outcome when the command is executed. For example, the word INPUT is a command in BASIC and is used to get a data from the user during program execution and then it assigns the value entered to the variable used with the INPUT command.
The language specifies how the command INPUT is to be used, there being several options; however, it must be followed in Toto.
Going back to the pseudo-code of computing the area of a circle, the actual program in BASIC language could be:
10 INPUT “Enter the Value of the Radius: “, R
20 LET PAI = 3.14
30 LET A = PAI * R * R
40 PRINT “The Area is: “; A
50 END
To translate the pseudo-codes or the instructions shown in the flow-chart to program codes one has to have a good grasp of reserved words, commands, functions, and other constructional rules defined in the respective high-level languages.
These have to be used exactly as per the details given in the manual, as these are also specific codes given in an easier-to-remember representation of the binary codes of 0s and 1s, which the translator has been told how to translate to what.
In certain high-level languages like COBOL, it is essential to write the program codes on special sheets called coding sheets, as the position of the instruction on a line also has some significance—these have to be started in each line at predefined columns.
However, these are not required in modern high-level languages like BASIC, PASCAL, C, etc., which have more or less free-form syntax. After coding, the instruction codes, called source code, are first stored in a file for ultimate conversion into executable programs.
v. Testing & Implementation:
The entered program, the source-code, is then “run” after being brought into a state of execution, to test its correctness, both in terms of syntax and logic; the former being done first. When an interpreter is used, the translator checks each line individually for correct syntax and then executes if it is found okay; otherwise, it points out the mistake.
When compilers are used, the total testing is done in one go and then all the mistakes in syntax are pointed out.
After all the mistakes in syntax have been corrected, the program is ready for use with actual data, but, before we can call the program correct, the logic part has to be tested inputting different types of data and manually checking whether the results being generated are correct. In large programs, such mistakes are not uncommon and so debugging is done to rectify the bugs [mistakes].
Debugging is the process of rectifying the logical mistakes in executable programs—the process of removing bugs. The basic difference between debugging and testing is that the mistakes found out by testing, executing the program with actual data, are removed during debugging, which is nothing but rectifying the mistakes in the logic of the program.
For example, when the values of two variables are to be added using a plus sign, if a sign of multiplication is used it will not be a syntactical error but a logical error and such mistakes can only be found by testing with actual data.
In fact, the software vendors, when they develop a specific software or revise an existing one, they hand it over to expert users for testing, generally called Beta-testing, when the bugs are found out and reported to the vendor for correction. In testing, wide variety of data are used to check the correctness of the program designed.
Essay # 3. Modular Programming:
In modular programming the main task is decomposed to different programming modules which are so designed that there is only one fixed entry and a definite exit point from a module. The main program, or even a sub-program, when it needs a specific task to be carried out, calls the concerned program module and hands over the control of execution-the sub program, a module, carries out the task and returns the control to the program that called it along with the results, if any.
The advantages of modular programming are:
i. As the main problem becomes decomposed to small programming modules, these can be easily programmed with chances of mistakes reduced to a minimum.
ii. All or the some of the modules can be simultaneously d by different persons, cutting down programming time. It adds flexibility to programming.
iii. Some of the frequently used modules of standard type can be kept in library files and used repeatedly with slight modifications only. Generally, these are related to input and out operations.
iv. The testing for detection of errors and debugging can be easily carried out, as the modules can be tested separately and individually.
Essay # 4. Preparing a Program Flow-Chart:
In any presentation of facts and figures for human understanding, graphical or pictorial representation has always a better impact on human mind. In view of this advantage, a number of techniques have been developed to represent different processing operations carried out on input data, to help the programmers understand the job of programming better.
On such graphical representation is called Flow Chart, which has many varieties. Hence, a flow-chart is a graphical representation of the various logical sequence of operations performed on input data to produce output information.
Using standard symbols, a flow-chart shows the flow of processing operations, required to be carried out to solve a programming problem. These standard symbols, approved by ANSI [American National Standard Institute], are used all over the world to convey the same meaning.
Some of the important symbols used are:
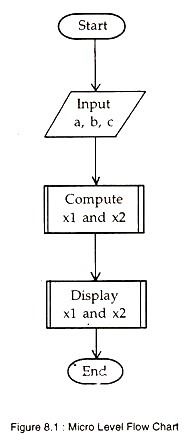
Using these three symbols, as shown above, a flow-chart can be prepared showing the broad processing sequences only—this being called a macro-level or high level flow chart. The purpose of this type of chart is to prepare the outline of the program, without being bogged down by details. An example would make this clear.
Suppose, we have to write a program to find the root of the quadratic equation: ax2 + bx + c = 0. As you all know from school days, the roots x1 and x2 are given by:
where a, b, and c are the coefficients.
In English, the code could be:
1. Get the values of a, b, and c.
2. Compute values of x1 and x2.
3. Display values of x1 and x2.
The corresponding flow-chart, which is at macro-level, will be as in Figure 1
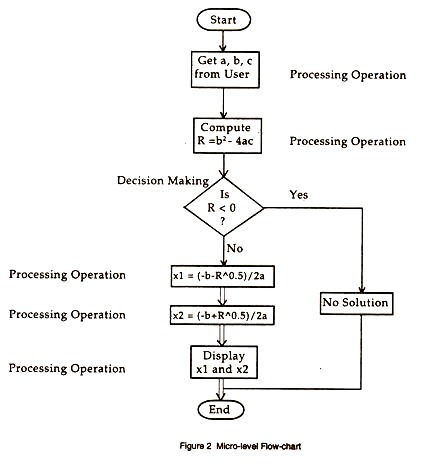
Once the macro-level chart is drawn, we can go in for the micro-level chart, which shows the detailed sequence of processing as will be actually required to solve the problem. Naturally, additional symbols are required, as invariably some decision making based on conditions would be required.
These symbols are:
There are many other symbols for use in System Flow Chart, we now being involved with Program Flow Chart, these are sufficient. Let us now modify the previous pseudo-code to find the roots of the quadratic equation at micro-level. Basically, the Step 2 of the previous pseudo-code will be enlarged.
Thus we have:
1. Get the values of a, b, and c.
2. Compute R = b2 – 4ac.
3. Is R negative, that is, R < 0? If yes, go to Step 7.
4. Compute x1 = (-b – R ^ 0.5)/2a
5. Compute x2 = (-b + R ^ 0.5)/2a
6. Display the values of x1, and x2 and go to Step 8.
7. Display “No solution”.
8. End
The micro-level program flow-chart will be:
Rules for Preparing Program Flow Chart:
To prepare a program flow-chart, the following rules must be followed:
1. There must be a definite Start/Begin and End positions, given by the appropriate symbols.
2. There will be a symbol for each operation—input, output, and processing [computations]; the details depending on the sequence.
3. When a decision is to be made, there must be two paths from it, taking care of both fulfillment and non-fulfillment of the condition stated.
4. There will be one decision symbol for each condition—the conditions cannot be combined.
5. A line, indicating the processing path, must start at a symbol and end at another symbol—it cannot be left dangling with a lose end.
6. Unless otherwise stated, vertical lines represent flow of processing from top to bottom of the page and horizontal line represents flow from left to right of the paper.
7. Where necessary, for shortage of space, a line may be broken by using connectors with proper matching notation, such as in one page and in the next page.
Advantages and Limitations of Program Flow Chart:
1. A program flow-chart clearly gives a visual display of the processing steps required to find a solution of a programming problem.
2. It forces a programmer to think logically and then draw a plan of execution on paper, without wasting valuable computer time and missing vital steps. Allows you to check the logical reasoning and evaluate the alternatives.
3. It clarifies what input data would be required and the how the output will be presented.
4. Since the program flow-chart is gradually built in steps, the scope for taking care of all the possibilities exist.
5. Using real-life data, a programmer can theoretically trace the steps leading to the solution and to check whether the algorithm used result in correct solution.
However, preparing program flow-chart for large complex problems is quite difficult and may result in confusion. Sometimes, it becomes difficult to convert a program flow-chart to appropriate program codes. Flow chart paths become too complicated when the number of conditions involved in data processing becomes larger in number.
Essay # 5. Decision Table for Pre-Programming Sequencing:
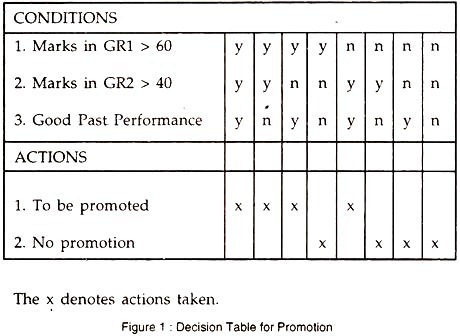
Decision tables are tabular representation of the actions to be taken under different logical conditions applicable to a program in such a manner that the correctness of the logic can be checked—it is an aid in pre-program sequencing. Decision Trees are graphical representation of decision tables.
The decision table has two parts, one containing the conditions and the other representing the actions to be taken. The condition part includes all the different conditions applicable to the data and the action part shows the different permitted actions depending on the conditions applicable in each case.
The columns in the table represent combinations of conditions and the rows represent the individual conditions; in the top-half of the decision tables. Let us take a simple example, where based on marks obtained in two groups of subjects, Group I [GR1] and Group 2 [GR2], and past performance, the decisions are to be taken to declare those promoted.
The corresponding decision table is given Figure 1:
Looking at the decision table, you can easily see which factors make a person eligible for promotion. Since each condition has two options, Yes and No, the total number of conditions to be handled is equal to 2n, where n is the number of conditions.
In this case, n = 3, therefore, there are 8 combinations. To prepare a decision table, the half-rule is followed, that is, first half of the number of choices is put as Yes, and the second half is put as No, the total number being decided by the position held by the condition.
For instance, in the example, Condition 1 being at top-most position of the three conditions, it has 23 = 8 options, so we have 4 Ys followed by 4 Ns. Condition 2 has 22 = 4 options, so two Ys are followed by two Ns, repeated for all cases. The third condition has only 2 choices of Y and N and these are repeated continuously. Once the conditions are laid out, the actions are determined based on the policy adopted.
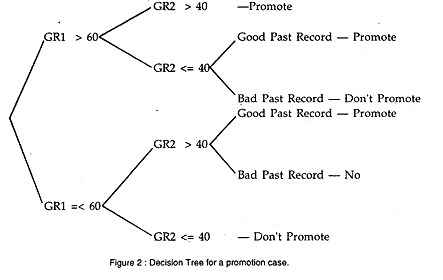
Although decision tables are useful, it becomes quite complicated to construct when the number of conditions become large. Decision Trees are useful in preparing decision tables.
The decision tree for the above example is given in Figure 2:
Essay # 6. Logical Instruction Used in Computer Programming:
Though logic in general stands for the science of reasoning, proof, thinking, or inference, in computer parlance logical instruction means arrangement of instructions in a step by step manner to successfully perform a desired task.
Obviously the logic depends on the task on hand. For example, to travel in the city of Calcutta by buses from Esplanade to Tollygunge we get into the appropriate bus and then pay for the ticket to the conductor.
So the logical instructions would be:
1. Get into the vehicle;
2. By the appropriate ticket.
As an alternative, we can also travel by the Metro Rail to go to the same destination from Esplanade to Tollygunge. But here if we do not buy the ticket before boarding the train, we are in for a hell of troubles. Incidentally, in both the cases, ticketless travelling is a punishable offence.
In this case, the logical instruction would be:
1. Buy the appropriate ticket;
2. Get into the vehicle.
The previous set of instructions get reversed here. In other words, the logical instruction formulated must take into account all the circumstances and provide for it. Incidentally, we have a sweet name for these kind of set of instructions —it is called Algorithm.
Originally, the term stood for doing arithmetic using Arabic [Indian?] numerical. At this stage, you would be entitled to ask what would be the correct algorithm to travel from one point to another using the city transports? Let’s see.
We could formulate the algorithm as:
Step 1: Is the vehicle of transport a rail? [Logical comparison]
Step 2: If yes, take Step 4. First and then Step 3
Step 3: Get into the vehicle
Step 4: Buy the appropriate ticket
With the computers, all instructions [steps] are executed serially one after another, unless specially altered. So if the answer to Step 1 is No [or False], Step 3 will be executed first and then Step 4. If the answer was Yes [or True], Step 3 will be executed after Step 4.
Let us take another concrete example involving arithmetic calculations, to illustrate what is meant by algorithm—all inclusive set of logical instructions leading to an answer. We take Euclid’s Algorithm, which is used to find the greatest common factor of two numbers.
In other words, if we have two whole numbers (integers) A and B, we have to find out a number C which would divide A and B without leaving any remainders.
Euclid’s Algorithm States:
1. Divide A by B to get the remainder C
2. If C is zero, make C = B, that is, B is the answer; End.
3. Make A equal to B and B equal to C and go to Step 1
Mind it, if we first make B equal to C and then make A equal to B, it will be incorrect because then both A, B, and C will be equal to each other having the same value of C.
Example 1:
To find the Highest Common Factor of 14 and 8, that is, A = 14 & B = 8. Let us solve the above using Euclid’s algorithm
Step 1: Divide 14 by 8, the remainder C = 6
Step 2: C is not 0, False: No action
Step 3: A = 8 and B = 6: Go to Step 1
Step 1: Divide 8 by 6, C = 2
Step 2: C is not 0, False: No action
Step 3: A = 6 and B = 2 : Go to Step 1
Step 1: Divide 6 by 2, C = 0
Step 2: C = B, that is C = 2 is the answer.
In the above problem data was 14 and 8, the desired information is 2, and the logical instruction was Euclid’s algorithm—the computer did an excellent job.
Computer programming, as it stands today, basically involves specifying what data would be processed by the computer using, which algorithms and other instructions to generate which information, ail in a language which the hardware understands—the program being called software.
Let us take another example to demonstrate what is meant by logical processing and how it is used.
Example 2:
The problem is to find out the grades, of students based on the marks obtained in different subjects in an examination. The gradation is based on the principle that an average mark of less than 40 [ <40 ] is “D”, between 40 and 59 is “C”, between 60 and 79 is “B”, 80 and above is “A”.
The algorithm could be:
1. Read all the marks of a student one by one — Input Data
2. Total the marks of the student — arithmetical operation
3. Divide the total by the number of subjects — arithmetic
Logical Operation:
4. Is the average marks < 40; if Yes, the grade is D. Go to Step 8
5. Is the average marks < 60; if Yes, the grade is C. Go to Step 8
6. Is the average marks < 80; if Yes, the grade is B. Go to Step 8
7. The grade is A.
8. Display the grade — Output Information
9. Go to Step 1
The same problem can be solved in many ways, but the one which uses the least number of steps, naturally, gives the fastest output. You try to solve this problem with marks being processed from higher side.
It should be obvious that for proper processing, correct logical instructions are required to be given, step by step in advance, which is generally stored in a file. If the instructions are incorrect, Garbage will be the output.
The general characteristics of an algorithm are:
1. There will be one unique initial action;
2. There will be finite sequence of a group of actions;
3. Each instruction will have a unique successor;
4. It will either end in solution or no-solution and will say so.
It must be clearly understood that algorithms are not available for all kinds of processing. The art of programming involves developing algorithms, coding them in computer languages and producing the required information from the data supplied—it is a highly specialized job and success to a large extent depends on the logical path specified.
But it is also not very difficult, if you know how to solve the problem in a systematic manner and the language the computer understands, to convert it to a program.